- Published on
【论文分享】|FlashOverlap:一种高效重叠通信和计算的轻量级设计
- Authors

- Name
- 耿浩哲
- GitHub
- @Hz188
FlashOverlap 所关注和聚焦的具体重叠场景是:一个计算操作后面跟着一个和计算结果存在依赖的通信操作(Overlapping Communication and Dependent Computation)
通信是并行的代价
如何重叠?
目前主流相关工作分为了两大类
一、基于张量分解的方法
思路:将依赖的计算和通信分为多个子操作,将子操作流水化执行
- 例如:矩阵乘法产生张量 T
- 分解为 N 个子矩阵相乘,得到 N 个子张量 T₁ ~ Tₙ,将一次对 T 的通信分解为对 N 个子张量的 N 次子通信
- 然后第 K 个矩阵乘法和第 K-1 个通信操作进行 Overlap
- 例如:矩阵乘法产生张量 T
限制与问题:切分存在要求。切分的子张量必须显存连续,才能直接调用 NCCL
- 导致:
- 为了保证切分出来的乘法结果的连续性,切分维度受限,难以支持 Tile-wise 的重叠
- 切分对计算性能有害,小矩阵乘法无法打满 GPU,导致子矩阵的计算耗时大于原先的矩阵乘法
- 导致:
二、基于算子融合的方法
思路:
- 将计算和通信融合为一个算子,挖掘 tile 之间的依赖
- 在 kernel 内部实现细粒度的通信和计算 overlap
限制与问题:
- 算子融合导致官方的高度优化的矩阵乘法、通信算子被打乱,对原有矩阵乘法和通信算子侵入过大,需要非常细致的优化和调整
- 导致开发难度大,耦合带来的复杂度高
- 针对不同的通信原语还要专门进行不同的开发和调优
一个高效且适应性强的重叠设计方案,应该满足:
- 支持 tile-wise 的重叠,以最大化重叠效果;
- 尽量少侵入计算部分,对计算无干扰,最小化对计算部分的伤害,保持原始的计算性能;
- 尽量对不同的通信原语和基于拓扑的优化技术正交,以最小化对通信部分的伤害,最小化不同通信原语的适配成本(人话:通信无关,减少针对不同通信原语的开发负担)
| 方法/特性 | Tile-wise 调度 | 计算侵入性 | 通信正交性 |
|---|---|---|---|
| 基于张量分解的方法 | ❌ | ❌ | ✅ |
| 基于算子融合的方法 | ✅ | ❌ | ❌ |
| 基于信号的方法 | ✅ | ✅ | ✅ |
新思路:基于信号的计算通信重叠方法
核心 idea:如果计算 Kernel 能够在完成一部分计算结果之后自动发出一个就绪的信号,然后接收到该信号之后我们发起一次针对就绪部分数据的 NCCL 的通信
一、基于信号的 overlap 实现机制
两个 Stream,一个 Stream 里是计算,另一个 Stream 里是通信。
- 在计算 Kernel 里轻量的加入一些 Flag 变量,当 “部分计算结果” 算完之后,将其对应的 Flag 置为 True。
- 与此同时,另外一个 Stream 里首先插入一个用于等待阻塞的 Kernel(几乎不占用计算资源),当该 Kernel 读到 Flag 置为 True 之后会退出,然后紧跟其后的通信算子被调用。
一个实际的 Timeline:

上图中计算流为轻量化加入 Flag 信号的 cutlass kernel,通信流中被打碎的通信部分,每一个 NCCL 通信之前有一个阻塞 Kernel 等待数据就绪。
二、“部分计算结果”如何界定
- 首先最直观和简单的设计是,每个 Tile 算完,我们就把结果发出来
Tile 的定义:矩阵乘法和其他重要计算在 CUDA 实现中的一个基本并行单元,矩阵 C 被分为了多个 Tile。
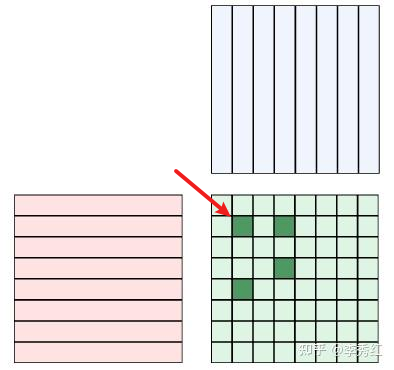
但每次发一个 Tile,小数据,性能不友好,通信带宽利用率低,调度和优化空间有限。
- 所以,积攒多个 Tile 一起
- 一起发就要求数据连续,Tile(block)执行顺序和完成顺序以及物理内存上的连续性无法保持一致。
- 比如:上图绿色的四个块,如果被选中为一组,就需要改成连续存储,才能通信。
- 为了保证正确性,引入了 MapTable
- 记录 Tile 应该存储的位置和步骤二引起的实际存储位置的映射关系。
- 模型的计算和通信后往往有 逐元素算子,将 map table 的逻辑融入到了逐元素算子中。
- map table 需要提前获取。
- 如何选取 tile 组
GPU 执行模型:N 个 block 的 kernel 发射到 GPU 上,GPU 会根据 kernel 编译期信息知道一个 block 占用的 SM 资源,从而知道一个 SM 可以并行执行的 block 个数。同时发射到 GPU 上的 block,在时间序列上呈现wave 现象,下图左 4 个 wave,图右两个 wave,实际上不会完全如此整齐划一的对齐,但相差不会太大。
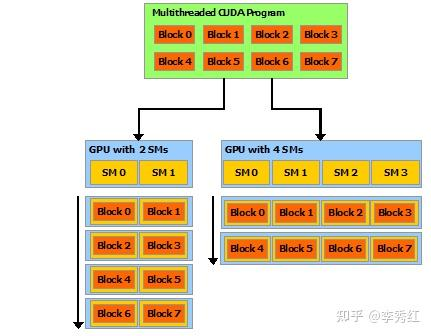
矩阵乘法也存在这种 wave 现象:每一个 wave 中包含的 tile 和 swizzling 算法相关。
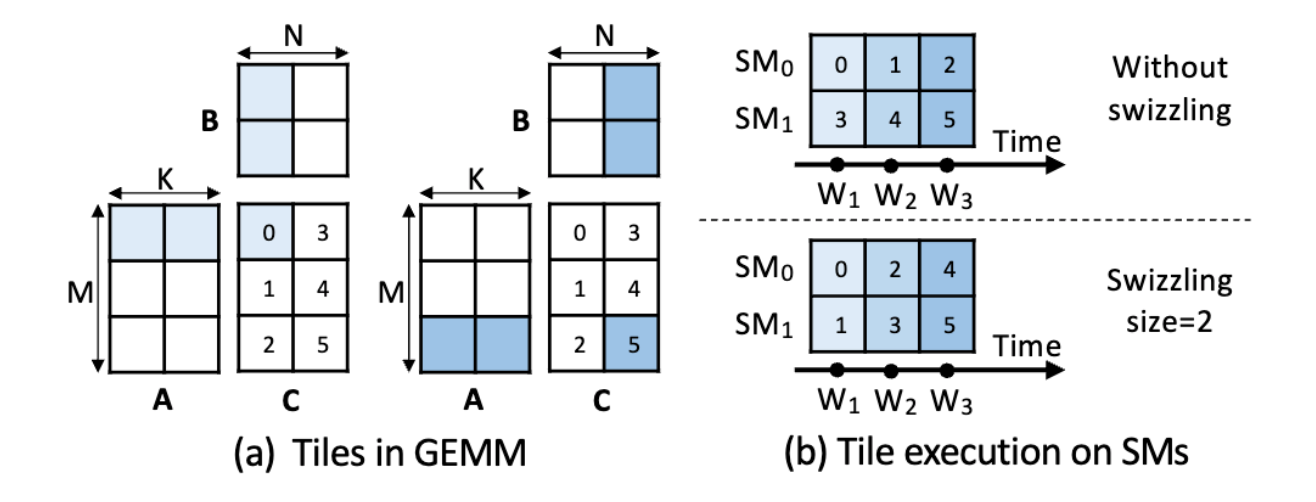
针对一个矩阵乘法进行观察结果如下图,横坐标是 block id,纵坐标是 block 完成时间:可以发现一个 wave 里的 block 的完成时间基本差不多,给选取 tile 组提供了事实依据。
- 选取同一个 Wave 的 Tile 作为一个组是一个非常不错的选择。这是由于同一个 Wave 内的 Tile 基本能整整齐齐的结束,很显然选择他们作为一个 Group,一起发一次通信效果会更好。
- 事实上是:当给定一个矩阵乘法和 GPU 之后,很容易提前得出 Block 的发射顺序从而获得 Wave 信息
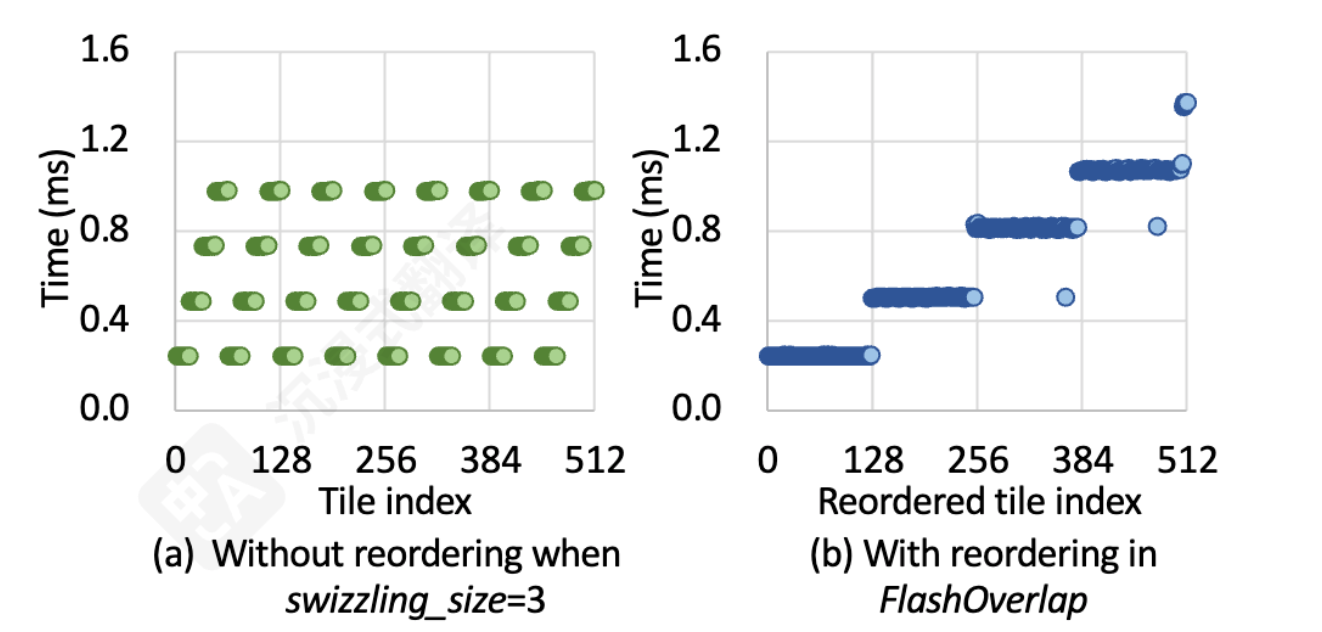
根据 gemm 的参数(tile 大小,swizzling 模式)提前生成 map table,记录 tile 到 wave 的关系(也就是提前知道了某个 tile 属于哪一个 wave)
上图是 RTX4090 上观察 wave 现象的结果图,C 矩阵有 512 个 tile,SM 数量 128 -> 512 / 128 = 4 个 wave
- 还观察到,tile 的完成顺序和内存地址是不对齐的(意思就是不是连续地址)
- 选一个 wave 作为 tile group 是不是最优选择
否,存在调优空间
- 一方面:希望一次通信数据要多,这样通信效率高,一个 group 尽量包含可能多的 tile;
- 另一方面:希望切分的要碎,算完就传,通信启动的越早越好,这样一个 group 尽量包含少的 tile。
存在 trade-off -> 调优出现了,通过调优选择合适的 tile group,具体调优过程提出了一个搜寻算法。
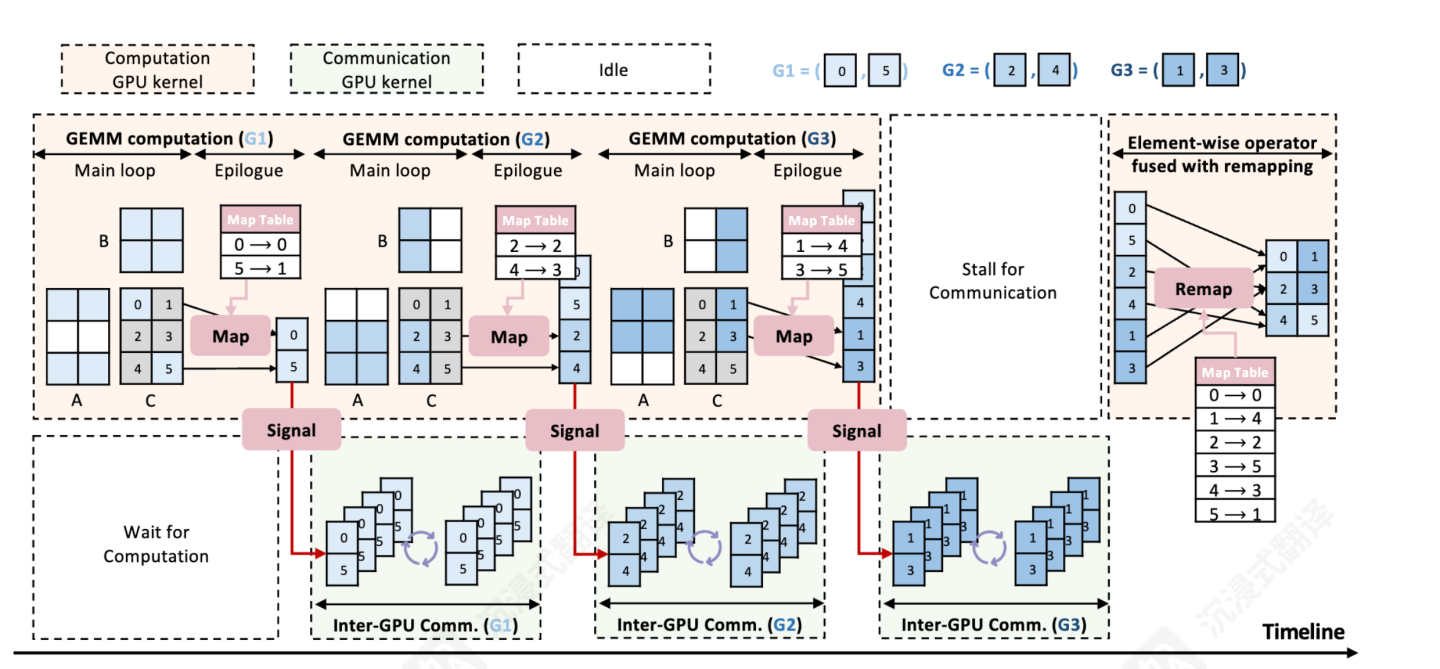
基于信号的计算通信 overlap 方案图
基于分解的 overlap 是 gemm 完成后通信,然后进行下一个分块的 gemm 再通信;基于融合的则是在 kernel 内部细粒度的调度计算和通信的执行。 这两种都要修改原生的 gemm 计算过程
本文方案:不改原生 gemm 计算流水、只轻量地添加一个 signal,另一个 stream 等 signal,等到了就启动通信
- 黄色:矩阵乘法;浅绿色:通信
- 示例包含 6 个 tile,分为了 3 个 group
- group1:tile0 tile5
- group2:tile2 tile4
- group3:tile1 tile3
- 每个 group 计算结束,就发起一次 NCCL 通信,同时将 map table 传到后面的逐元素算子,回复对重映射的影响
“设计空间”
tile -> wave -> wave group 如何确定每个 group 的大小?
波组内波的个数如何界定的方式 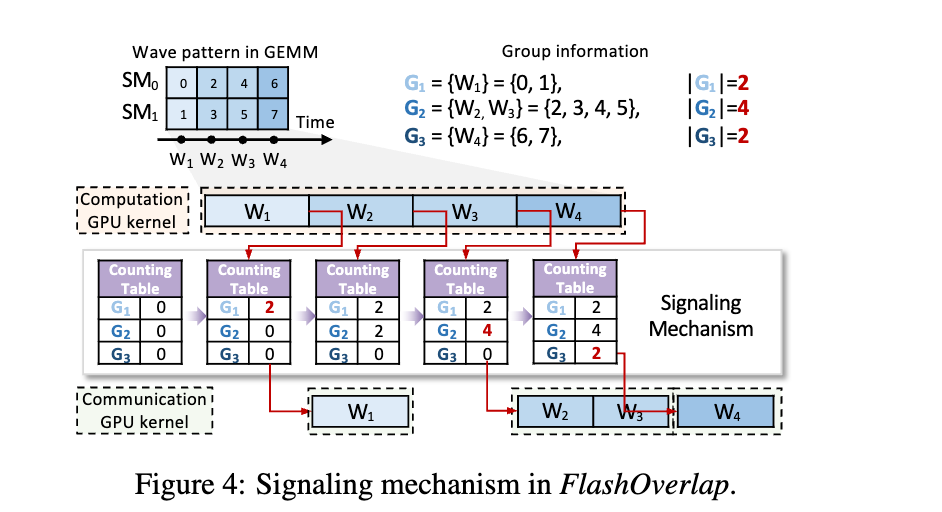
- 引入了一个 tile 计数表 来 track 矩阵的计算过程,按 group 记录完成的 tile
- 计数表长为 P,表示 tile 被分进了 P 个 Group G_1 ... G_P
- 当 G_i 中的 tile 完成,则 G_i 表项+1,如果这个值达到|G_i|这个设定值,那么通信开启,Flashoverlap 通过 tile 索引判定属于哪个 group
Flashoverlap 不在 tile 触发通信,也不在 wave 触发通信,而是在完成了几个 wave(wave group)时触发通信 为了保证连续性,在通信前会 reorder 将数据写入连续地址,通信后会 reorder 复原 wave group 的大小选择 -> 组成了一个设计空间,论文提出了一种基于预测模型的预测搜索
调优必要性
把一次一个 wave 作为 group 通信作为 baseline 进行观察,这种方案是最细粒度的 overlap,发现无法提供最佳性能
- 4090 上测了 50 个形状的 gemm,只有 4% 基线是最优,平均有 17% 的性能下降
- 原因:分段的通信带宽利用率低,频繁调用通信 api 开销大
所以,不同的 wave 分区对整体 overlap 的性能有很大影响,需要调优
直接调优开销巨大
M=4096,N=8192,K=7168 -> 1024 个 tile(256*128)
4090 有 128 个 SM,1024/128=8 个 wave -> T=8
所以有 2^{8-1}=128 中 wave group 的分区方案,在线执行并 profile 的时间超过一分钟,端到端系统不可接受
实时调优方法
提出了一种预测搜索方法,去解决 wave 该如何 partition,将设计空间从 2^{T-1} -> O(2^{T-2}),通过一种延迟预测器替代的线上 profile
- 所谓 2^T-1 的意思就是,如果我们有 T 个波,那么我们将有这么多种分 group 的方案,对每中方案都做 online profile 代价太大,端到端不可接受
- 通过这两个方法能够实时的生成 wave 的 partition
方法: 通过先验知识,进行缩减
- 考虑一个该方案的正常时间线,重叠的计算和通信部分,占据了中间的大部分时间线,因此头尾两个单独的非重叠部分对整个时间线有着比较大的影响,所以最后一个和第一个 group 不能过大,避免冷启动和长尾问题,从而缩减了设计空间的大小
将 online profile 替换成一个预测延迟的 cost model
最终算法

离线阶段
- 根据 GPU 信息、矩阵信息,得到 wave 个数
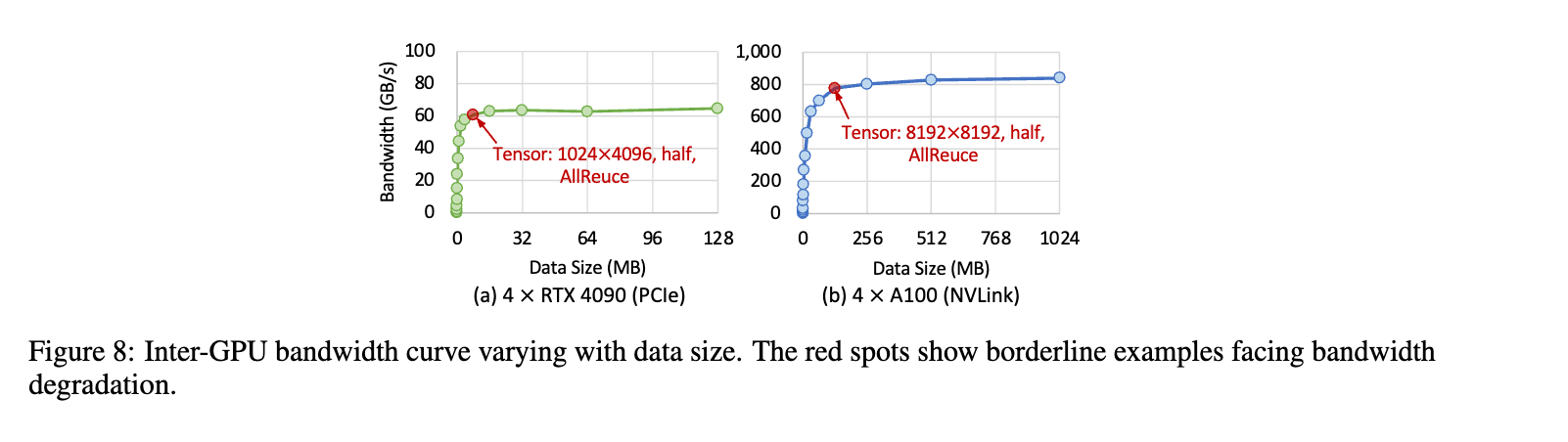
- 根据通信类型,通信数据大小,得到通信曲线
注意资源的竞争,用于 gemm 的 sm 个数是减去掉 nccl 占用的 sm 个数的
在线阶段
- 根据 wave 个数,产生一种 wave partition 的候选 (2^(T-1)中的一种)
- 预测性搜索最优的 group partition 方式
实现
gemm
- 通过 cutlass 的 gemm 实现了
- 保留了计算主循环
- tile 顺序的 re map 过程融入到了 gemm 的 epilogue 中,避免主循环性能下降(轻量)
信号机制
- 使用 cuda kernel 实现,定期查计数表
通信
- NCCL api
计算 + 通信
- 通过 cuda stream 管理
效果与性能
FlashOverlap 提供了 69‑98% 的理论性能,并通过计算 ‑ 通信重叠实现了高达 1.65× 的加速。 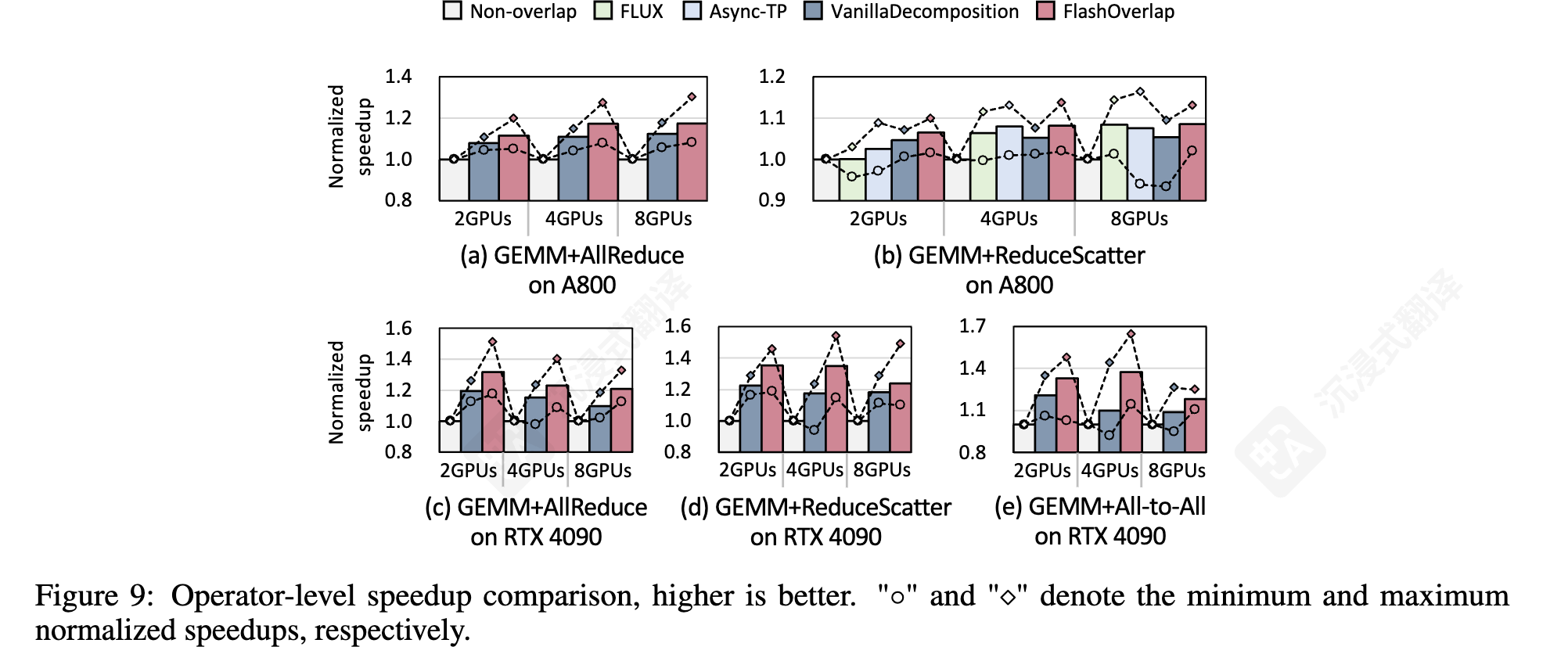
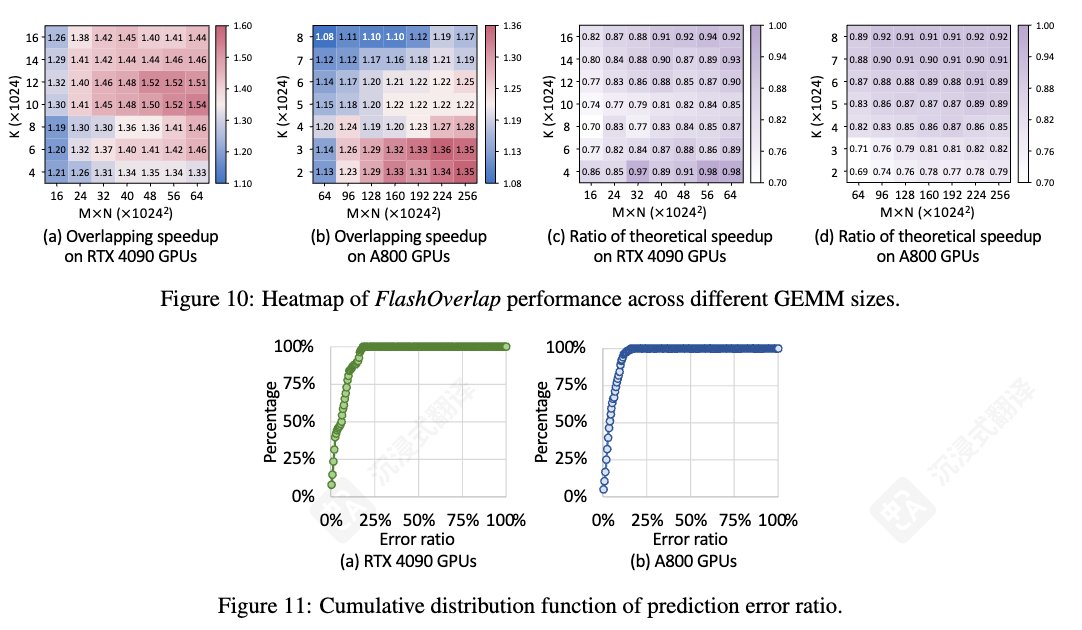
图 10:在大多数情况下,FlashOverlap 实现了超过 80% 的理论加速比。由于( 1 )分段通信导致带宽利用率低下和( 2 ) SM 竞争导致的计算延迟延长,该比率低于 1
图 11:
- 平均误差比分别为 3.41% 和 3.44%
- 比较了搜索分区和最优分区之间的性能。基于高精度的预测器,搜索分区实现了最优分区的 > 99% 性能
核心观点和 Feature
- 如果计算 Kernel 能够在完成一部分计算结果之后自动发出一个就绪的信号,然后接收到该信号之后我们发起一次针对就绪部分数据的 NCCL 的通信。
- 分解的 overlap 方式存在难以支持 tile-wise 重叠、对计算效率有害的问题,融合的 overlap 方式存在开发难度大,侵入强的问题。
- 一个高效且适应性强的重叠设计方案,应该满足三点:
- 支持 tile-wise 的重叠,以最大化重叠效果;
- 少侵入计算部分,对计算无干扰,最小化对计算部分的伤害,保持原始的计算性能;
- 通信无关化,以减少针对不同通信原语的开发负担(通信无关的设计使得 FlashOverlap 能够通过标准 API 调用直接利用 NCCL 的通信,甚至也可以调用 mscclang 和 deepep)
可能有什么优化方向、有哪些优化的可能
目前刚开始读这方面的论文,积累不足,主要起到一个抛砖引玉的作用,大家多多讨论,跟大家多学习
- 通信无关性这点,应该也可以结合 nvshmem 进行通信,可能在某些场景比 NCCL 更好一点